Exploring Tree Traversals: Depth-First Search and Breadth-First Search Algorithms

Trees are like models of hierarchical data, such as file systems, family trees, and organizational charts. In my laGst articles, I talked about the basics of building trees and binary search trees, which are important data structures in computer science. If you haven’t read them check these out,

• Exploring on tree data structures
• Understanding binary search trees

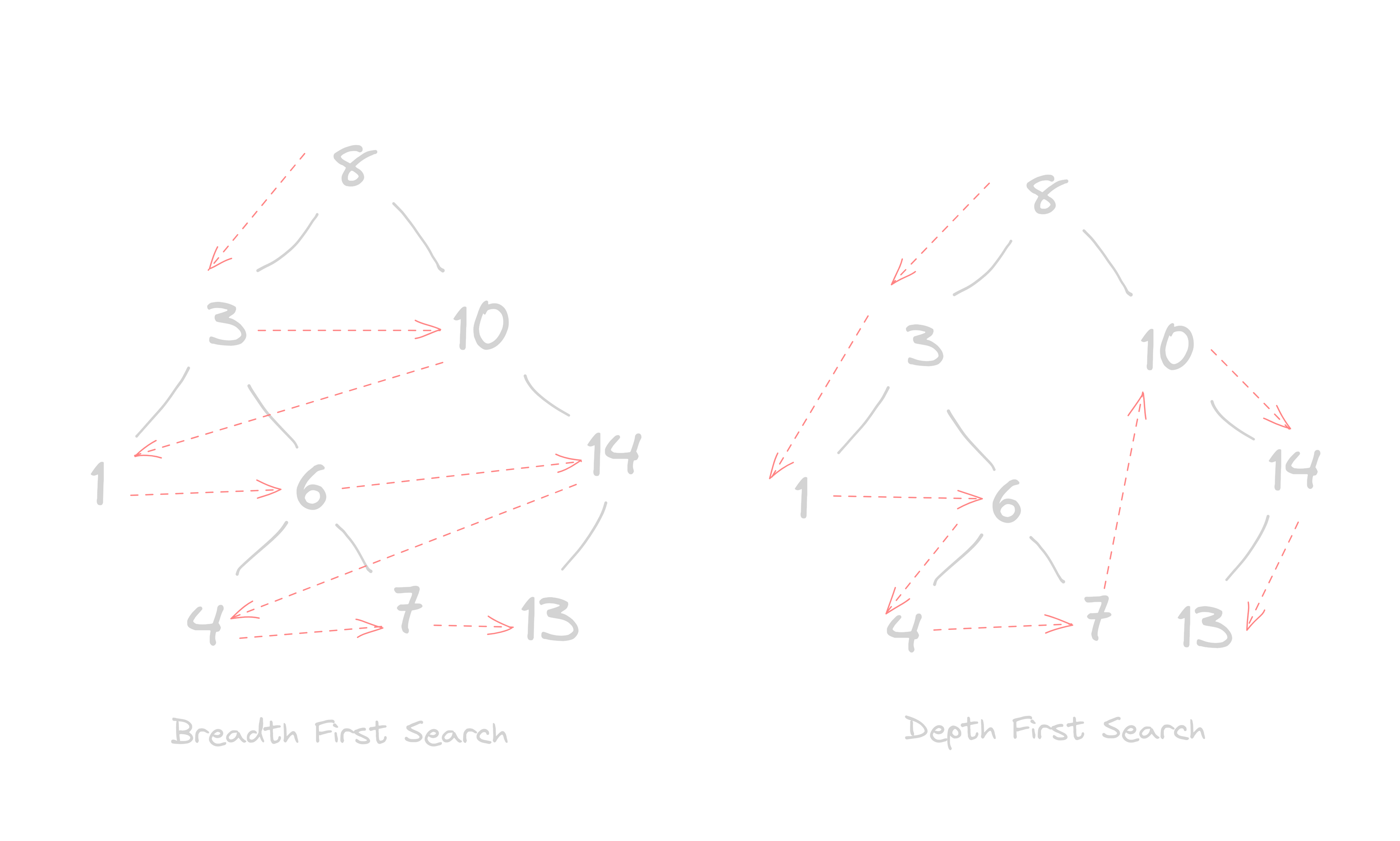
Let’s take a look at how you can traverse a tree by visiting each node in a particular order. Traversing a tree can be done using different methods, depending on what you want to achieve. Two common traversal algorithms are depth-first search (DFS) and breadth-first search (BFS). DFS goes as deep as possible in a branch before coming back to check other branches. BFS checks all nodes at the same level before moving to the next level.

Depth First Search

Depth-first search is a way to move through a tree or other graph. You keep going down one path until you can't anymore. While you're moving, you keep a list of where you're going next in a stack. If you don't know what a stack data structure is, you can read my article about it here . You always choose the most recent thing you added to the stack first. If you hit a dead end, you go back to the last place where there were other options and try one of them instead. You keep doing this until you've been to all the nodes in the graph.

Three Types of Depth First Search

There are three main ways to implement a depth-first search:

• Pre-order traversal: This traversal visits the current node before visiting any of its children.
• In-order traversal: This traversal visits the left subtree, then the current node, and finally the right subtree.
• Post-order traversal: This traversal visits the left subtree, then the right subtree, and finally the current node.

Each of these traversal patterns has its use cases depending on the specific problem you are trying to solve.

Pre order traversal

In pre-order traversal, the algorithm visits the current node before visiting any of its children. This method is used in tree traversal, where we visit each node of a tree exactly once. In this algorithm, we begin by visiting the root node, then recursively traverse the left subtree of the node, and finally the right subtree.

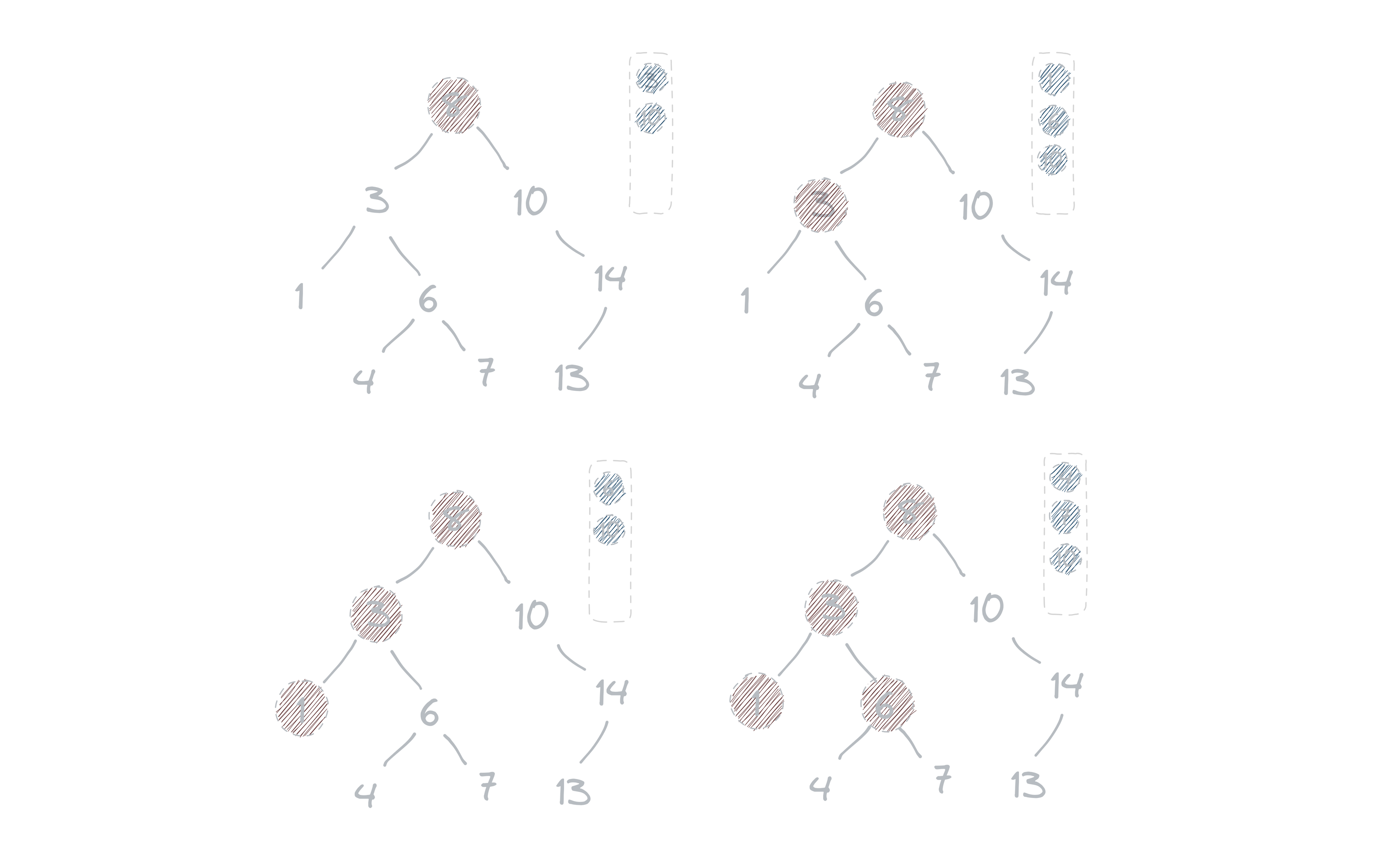
Visit 8, add 8 to the array,
// Stack - [] | Array - [8]
add 3, 10 to the stack
// Stack - [3, 10] | Array - [8]
visit 3, add 3 to the array,
// Stack - [10] | Array - [8, 3]
add 1, and 6 to the stack
// Stack - [1 ,6 , 10] | Array - [,8, 3]
visit 1, add 1 to the array
// Stack - [6, 10] | Array - [8, 3, 1]
visit 6, add 6 to the array
// Stack - [10] | Array - [8, 3, 1, 6]
add 4 and 7 to the stack
// Stack - [4,7,10] | Array - [8, 3, 1, 6]
visit 4 add 4 to the array
// Stack - [7,10] | Array - [8, 3, 1, 6, 4]
visit 7 add 7 to the array
// Stack - [10] | Array - [8, 3, 1, 6, 4, 7]
// and we continue until the stack is empty

const preOrderTraversal = (node: Node | null, array: number[]) => {
  if (!node) return array;
  array.push(node.value);
  array = preOrderTraversal(node.left, array);
  array = preOrderTraversal(node.right, array);
  return array;
};

If you are not familiar with how stacks work check out my other article on Stack data structure with arrays and linked-lists .

In-order traversal & post-order traversal

In in-order traversal, each node is visited in a specific order. First, the left subtree is visited, then the current node, and finally the right subtree. This method is used to visit each node in the tree in ascending order. In-order traversal is one of the three main methods for traversing binary trees, along with pre-order and post-order traversals. It is particularly useful for binary search trees, where the elements are ordered in a specific way to allow for efficient searching. In-order traversal can be used to create a sorted list of the elements in the tree. In post-order traversal, the algorithm visits the left subtree, then the right subtree, and finally the current node.

const inOrderTraversal = (node: Node | null, array: number[]) => {
  if (!node) return array;
  array = inOrderTraversal(node.left, array);
  array.push(node.value);
  array = inOrderTraversal(node.right, array);
  return array;
};

const postOrderTraversal = (node: Node | null, array: number[]) => {
  if (!node) return array;
  array = postOrderTraversal(node.left, array);
  array = postOrderTraversal(node.right, array);
  array.push(node.value);
  return array;
};

Breadth-First Search

Let’s talk about breadth-first search, BFS is a graph traversal algorithm that is similar to depth-first search, but with a few notable differences. The main difference is that breadth-first search uses a queue to keep track of what to look at next, while depth-first search uses a stack.

Check out more about queues here - Queues : From Waiting in Line to Queuing Up

Breadth-first search explores all the vertices at the current level before moving on to the next level, while depth-first search explores as far as possible down a single branch before backtracking. Breadth-first search is often useful for finding the shortest path between two vertices in an unweighted graph, as it is guaranteed to find the shortest path if one exists. It also has applications in network routing protocols and other areas.

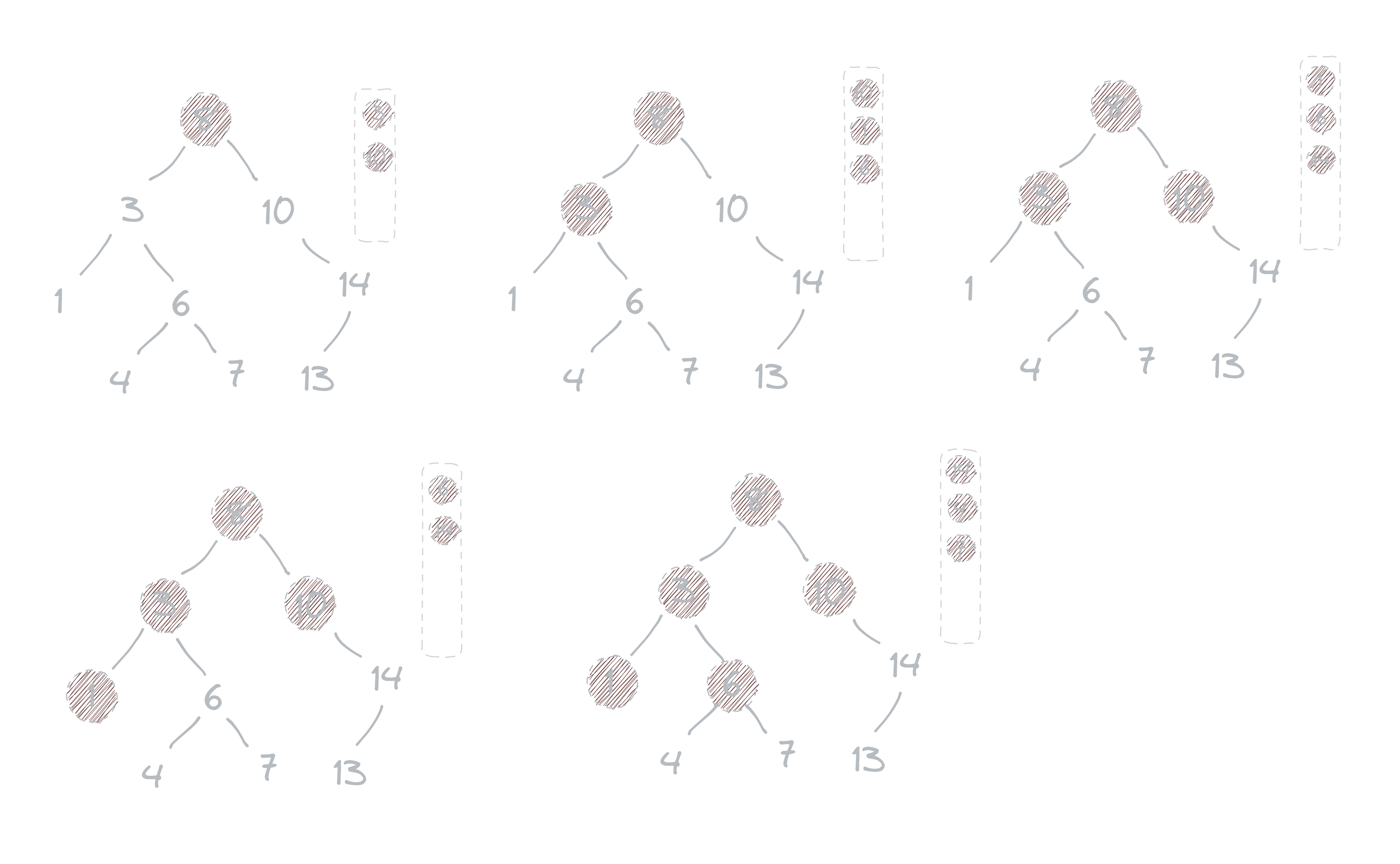
As we search, we see that it has some clear advantages: we look at many topics rather than just a few in depth. For example, we might look at five types of grinders before diving into each one's history and inventor. This type of search is good for people who like to move quickly from one thing to another and not spend too much time on any one topic.

Another example of using breadth-first search is in finding the shortest path between two points on a map, which I will be writing about later in my blog. By exploring all possible routes at the same distance from the starting point, we can be sure to find the shortest path once we reach the destination. This method is used in many navigation apps to provide users with the most efficient route possible. Since both depth-first search and breadth-first search only explore one option at a time, they work at the same rate.

function breadthFirstTraversal( queue: Node[], arr: number[]){
    if(!queue.length) return arr;
    let node = queue.shift()
    arr.push(node.value)
    if(node.left) queue.push(node.left)
    if(node.right) queue.push(node.right)
    return breadthFirstTraversal(queue,arr)
}
function breadthFirstTraversal( queue: Node[], arr: number[]){
    while(queue.length){
        const node = queue.shift()
        arr.push(node.value)
        if(node.left) queue.push(node.left)
        if(node.right) queue.push(node.right)
    }
    return arr
}

Related Articles

Implementing Heaps : A Comprehensive Guide

Learn how to create a min heap and their operations

Creating and traversing tries

Tries, also known as prefix trees, are tree-like data structures used for quick string searching.

Exploring more on tree data structures

A helpful guide for anyone interested in learning more about tree data structures, their behavior, and their applications in various fields.