Understanding Binary Search Trees: A useful guide
Jun 7, 2023Arkar
CS
Detailed explanation of adding, removing and searching values in a binary search tree.
On this page
When I finally decided to dive into data structures, I was overwhelmed by how trees work. It's not just about understanding what a tree is, but also about the different types of trees and the various ways they can be used.
Binary trees and AVL trees are two types of trees with distinct properties. Trees can be employed to represent various data structures, including file systems, programming language syntax trees, and others. Though understanding trees might be initially perplexing and complicated, it is important to have a solid grasp of them to become a skilled programmer. In this article, I will be mostly focusing on how binary search trees work
Trees are structures made of nodes that are linked together. Each node has two branches that lead to other nodes. Trees are a lot like linked lists, but instead of just one list, there are many lists branching off each other.
A binary search tree has nodes that can have a left or right child, but no more than two children. In binary search trees, the left child is always smaller than the parent, while the right child is always larger. This lets us quickly find and sort data in the tree.
class Node {
value: number;
left?: Node;
right?: Node;
constructor(value: number) {
this.value = value;
this.left = null;
this.right = null;
}
}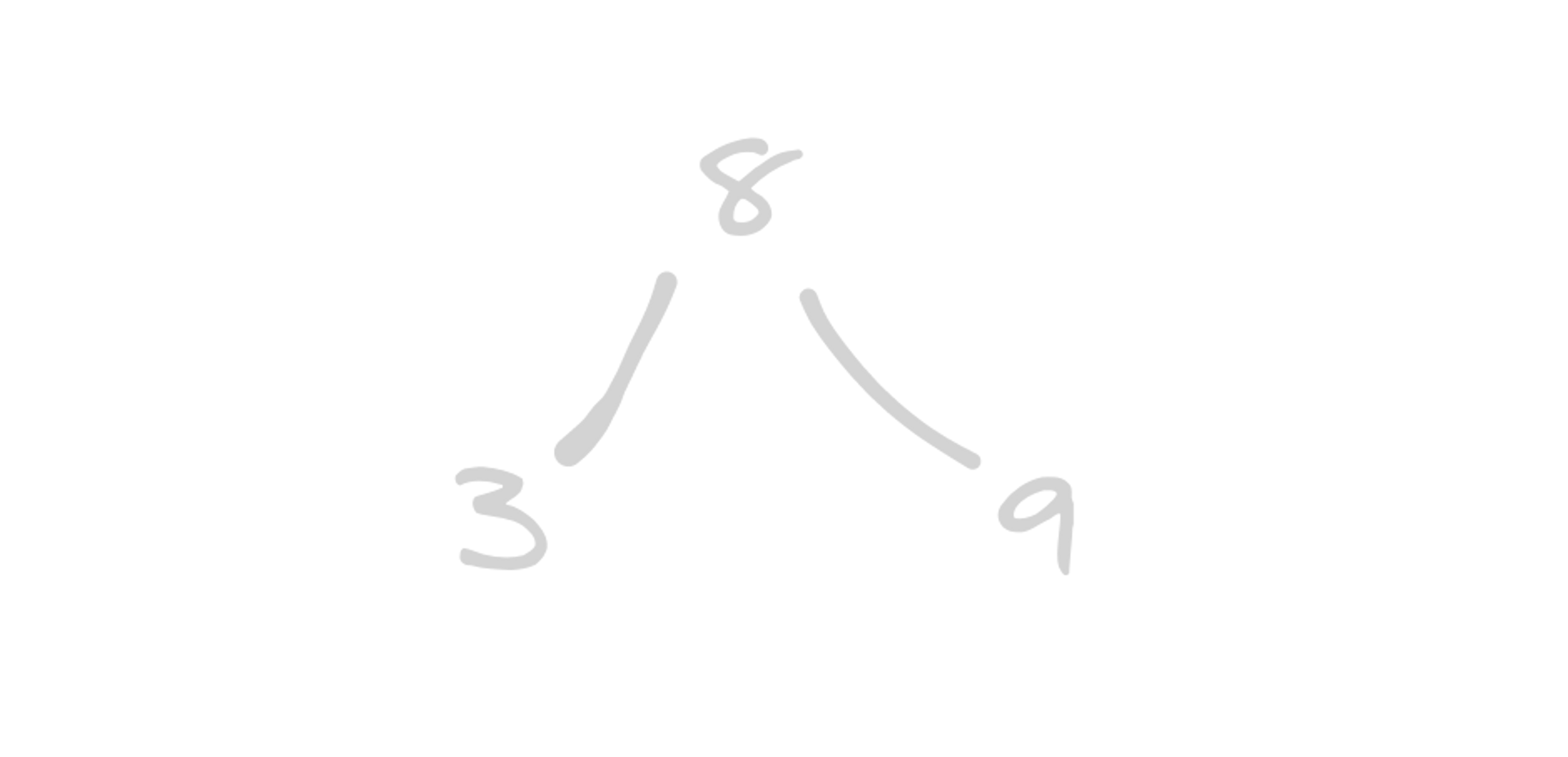
Binary search trees start at a single root node at the top of the tree and branch into multiple paths as they descend. The topmost node of a binary search tree is called the root node. It does not have a parent node and is where you start when traversing the tree. Values that are equal can be placed on either side, as long as it is consistent.
class BST {
root?: Node;
constructor() {
this.root = null;
}
}Adding Values to Binary Search Tree
To add a new value to a binary search tree, follow these steps:
- Start at the top of the tree (root node).
- Compare the new value to the current value.
- If the new value is less than the current value, go left.
- If the new value is greater than the current value, go right.
- Repeat until you reach an empty spot where the new value can be added.
push(value: number) {
let newNode = new Node(value);
if (this.root === null) {
this.root = newNode;
return newNode;
}
let tmp = this.root;
while (true) {
if (value < tmp.value) {
if (tmp.left === null) {
tmp.left = newNode;
return newNode;
}
tmp = tmp.left;
} else {
if (tmp.right === null) {
tmp.right = newNode;
return newNode;
}
tmp = tmp.right;
}
}
}To add a value to the tree, we first create a node with the value we want to add. If the tree is empty, we set the new node as the root node and return it. If the tree is not empty, we compare the value we want to add to the current node's value. If the value is less than the current node's value, we move to the left child. If the value is greater than the current node's value, we move to the right child. We repeat this process until we find a spot where we can add the new node.
This way of adding a value to a binary search tree is fast. It only checks each node once and stops going down the tree when it finds an empty place. That means adding a value takes O(log n) time, where n is the number of nodes in the tree.
Searching values to Binary Search Tree
To search for a value in a binary search tree, follow these steps:
- Start at the top of the tree (root node).
- Compare the search value to the current value.
- If the search value is equal to the current value, return the current node.
- If the search value is less than the current value, go left.
- If the search value is greater than the current value, go right.
- Repeat until you find the search value or reach a null node.
search(value: number) {
if (this.root === null) return -1;
let tmp = this.root;
while (true) {
if (value === tmp.value) return tmp;
if (value < tmp.value) {
tmp = tmp.left;
} else {
tmp = tmp.right;
}
}
}To search for a value in a binary search tree, you can follow these steps:
- Start at the top of the tree (root node).
- Compare the search value to the current value.
- If the search value is equal to the current value, return the current node.
- If the search value is less than the current value, go left.
- If the search value is greater than the current value, go right.
- Repeat steps 2-5 until you find the search value or reach a null node.
A binary search tree is designed so that each node has at most two children. The left child is always smaller than the parent, while the right child is always larger. This structure makes searching for a value in a binary search tree quick. The search only checks each node once and stops going down the tree when it finds the value it is looking for or reaches a null node. This means that searching for a value takes O(log n) time, where n is the number of nodes in the tree.
Searching element recursively
function recursiveSearch(node: Node, value: number) {
if (node.value === value) return node;
if (value < node.value) return recursiveSearch(node.left, value);
if (value > node.value) return recursiveSearch(node.right, value);
}When searching for an element in a binary search tree, one approach is to use recursion. Recursively means you keep using the same function to look at smaller and smaller parts of the tree until you find what you're looking for. Recursion is easier to write because it takes less code, but it can be slower for big trees because it uses up a lot of computer memory.
Removing nodes from a binary search tree
Removing nodes from a binary search tree is a more complicated process then adding them.
- Removing a leaf node (with no children)
- Removing an internal node with a single child
- Removing an internal node with two children
I will cover all three of them and help you get a grip on how things work.
Removing a leaf Node
When you remove a node from a binary search tree, you have to make sure the tree remains a valid binary search tree. Remember, the golden rule for a binary search tree is that the left child needs to be smaller than the right child, or consistent in this manner. After removing a node, the left child must be smaller and the right child must be larger than the parent.
Removing a leaf node is a matter of simply deleting the node from the tree. There is no need to worry about maintaining the structure of the tree since leaf nodes have no children.
remove(value: number) {
// the tree is empty
if (this.root === null) {
return false;
}
// start at the root node
let current = this.root;
let parent = null;
// start traversing the tree
while (current) {
// found the value
if (value === current.value) {
// we are good its a leaf node
if (current.left === null && current.right === null) {
// if the node is the root node
if (current === this.root) {
this.root = null;
} else if (current === parent.left) {
// if the node is the left child of its parent
parent.left = null;
} else {
// if the node is the right child of its parent
parent.right = null;
}
return true;
}
}
// we keep traversing
parent = current;
if (value < current.value) {
current = current.left;
} else {
current = current.right;
}
}
//If we did not find the value we wanted to remove
return false;
}
To remove a node from the tree, we traverse down the tree to find it and then delete it. We can delete a leaf node simply, but let’s see how we can remove it with one child.
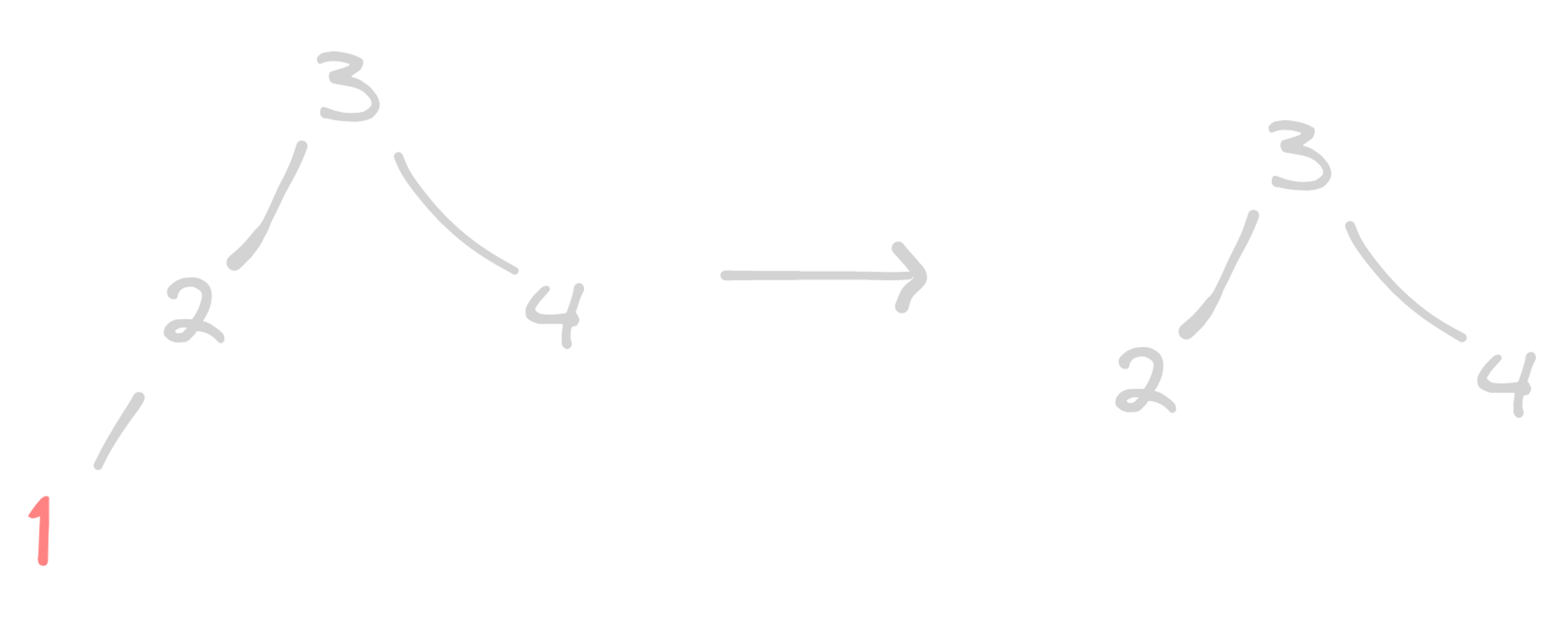
Removing with one child
To remove a node with one child from the tree, we need to make sure that the child of the removed node takes its place in the tree. If the node has a left child, we need to set the parent of the removed node to point to the left child. If the node has the right child, it can just go to the right!
remove(value: number) {
//The tree is empty
if (this.root === null) {
return false;
}
// start at the root node
let current = this.root;
let parent = null;
// start traversing the tree
while (current) {
// found the value
if (value === current.value) {
// if the node has only one child
if (current.left === null || current.right === null) {
let child = null;
if (current.left !== null) {
child = current.left;
} else if (current.right !== null) {
child = current.right;
}
// if the node is the root node
if (current === this.root) {
this.root = child;
} else {
// if the node is the left child of its parent
if (current === parent.left) {
parent.left = child;
} else {
// if the node is the right child of its parent
parent.right = child;
}
}
return true;
}
}
// we keep traversing
parent = current;
if (value < current.value) {
current = current.left;
} else {
current = current.right;
}
}
//If we did not find the value we wanted to remove
return false;
}To remove a node with one child, we follow the same process. We find the node to remove and then check if it has a left or right child. For the left child, we just point it’s parent to the left, and the same thing for the right.
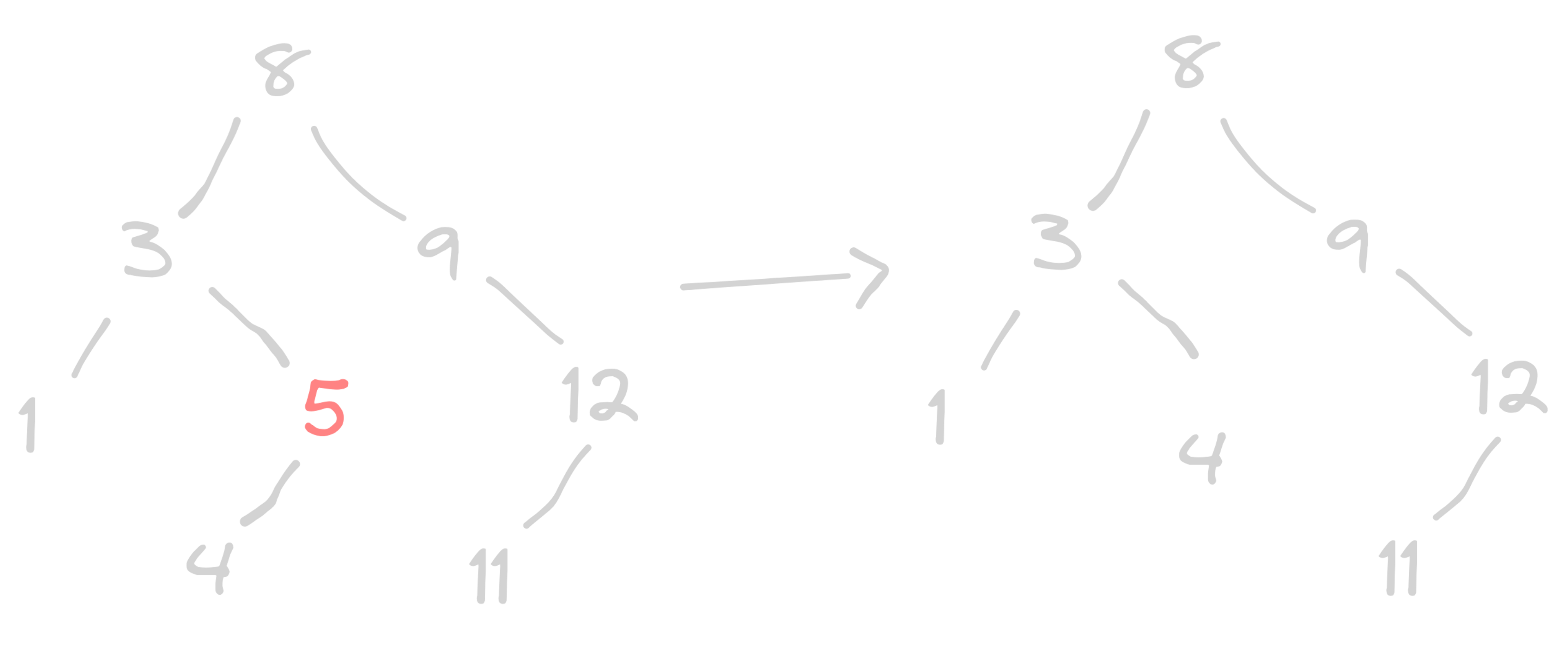
Removing with two children
To remove a node with two children,
- Find the node with the next highest value (usually the smallest value in the right branch).
- Copy the value of the replacement node to the node we want to remove.
- Remove the replacement node from the tree.
remove(value: number) {
// the tree is empty
if (this.root === null) {
return false;
}
// start at the root node
let current = this.root;
let parent = null;
// start traversing the tree
while (current) {
// found the value
if (value === current.value) {
// and it has two children
if (current.left !== null && current.right !== null) {
// get the smallest in the right branch
let replacement = current.right;
while (replacement.left !== null) {
replacement = replacement.left;
}
// copy the value of the replacement node to the current node
current.value = replacement.value;
// remove the replacement node from the tree
value = replacement.value;
current = replacement;
}
/**
* will have two techniques above here
*/
}
// we keep traversing
parent = current;
if (value < current.value) {
current = current.left;
} else {
current = current.right;
}
}
//If we did not find the value we wanted to remove
return false;
}
When removing a node with two children, we replace the target node with the replacement node. The replacement node is the node with the next highest value, which is the smallest value in the target node's right branch. We copy the value of the replacement node to the target node and then remove the replacement node from the tree.
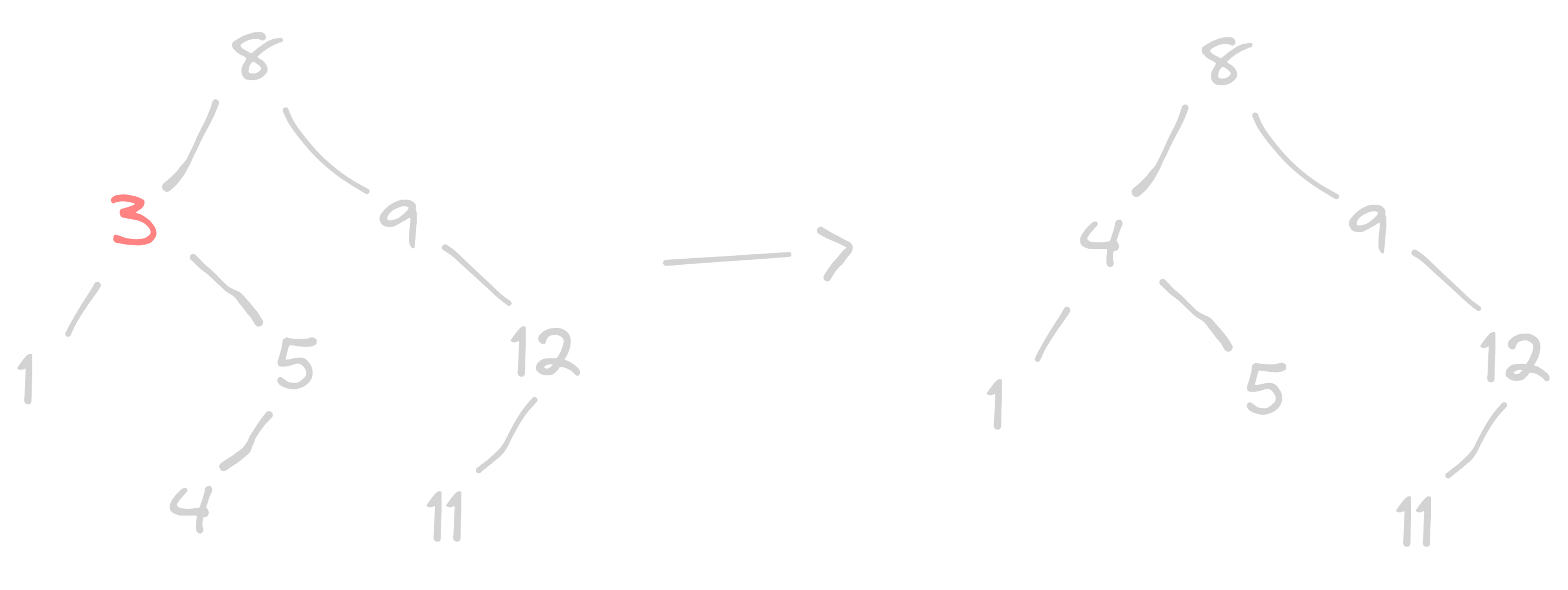
Big O in binary search trees
The thing about binary search trees is that the big O of binary search trees depends on the tree's height. If the binary search tree is balanced, it has O(log n) time complexity for searching, inserting, and deleting. This is similar to linear search in an ordered list. Check out my However, if the binary search tree is unbalanced, it can degenerate into a linked list(Check out my other article about Linkedlists ), in which case the time complexity for searching, inserting, and deleting becomes O(n), which is significantly slower.
10
/ \
7 15
/
6
/
5
/
2I am not gonna talk about how to deal with such a problem in this article this is long enough already to get you bored. In the next article, I will be writing about Self-balancing trees, such as AVL trees which can automatically maintain a low height and fast search times. They are useful in cases where the stored data is constantly changing, like in databases or file systems. Self-balancing trees guarantee a worst-case time complexity of O(log n) for operations like searching, inserting, and deleting, irrespective of the stored data.
Bulk Construction of Binary Search Trees
When constructing binary search trees with a large number of nodes, it is more efficient to use a bulk construction algorithm rather than adding each node iteratively. For example, using sorted arrays to create a binary search tree. This is called a bulk construction of binary search trees. We just then take the middle node as the root of the tree. The left and right subtrees are then constructed recursively, using the left and right halves of the array, respectively. This algorithm has a time complexity of O(n log n) and a space complexity of O(log n), If you want more on how you can sort arrays check out my other articles on sorting in programming.
function sortedArrayToBST(arr: number[]): Node {
if (arr.length === 0) {
return null;
}
let mid = Math.floor(arr.length / 2);
let node = new Node(arr[mid]);
node.left = sortedArrayToBST(arr.slice(0, mid));
node.right = sortedArrayToBST(arr.slice(mid + 1));
return node;
}
Trees are used everywhere in programming. And they can be overwhelming for someone to get started with. Trees represent file system and programming language structure. The Document Object Model (DOM) uses trees to represent the structure of HTML, CSS, and JavaScript code in web pages. Learning about binary search trees can change how someone thinks about programming. Data structures help you understand trade-offs between time and space complexity and make design decisions for faster and more scalable applications.
Subscribe to my NewsLetter!
Join my web development newsletter to receive the latest updates, tips, and trends directly in your inbox.
Related Articles
Implementing Heaps : A Comprehensive Guide
Learn how to create a min heap and their operations
Creating and traversing tries
Tries, also known as prefix trees, are tree-like data structures used for quick string searching.
Exploring Tree Traversals: Depth-First Search and Breadth-First Search Algorithms
Take a deep dive into the world of tree traversal with this article, which covers both depth-first and breadth-first search algorithms.
On this page